Matriz de accesibilidad de un Digrafo en c++ – Virginia – Platform – cancer

ParaDigrafos existe un procedimiento para encontrar lamatriz de accesibilidad, podemos determinar la matriz de accesibilidad a través de una serie de pasos. La matriz de accesibilidad nos brinda información sobre si el digrafo es F.C (fuertemente conexo) o no, es decir si para cada par de vértices u,v:u es accesible desdev yv es accesible desdeu.

Al observar la matriz sí notamos que hay al menos un elemento igual a cero diremos que el digrafo no es F.C conexo. De lo contrario, si es F.C.

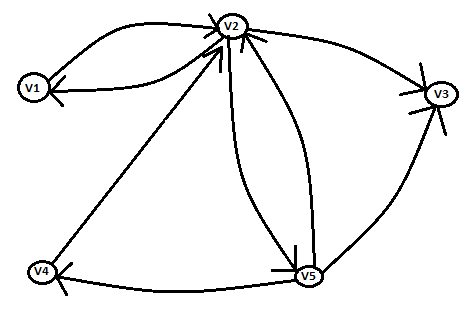
La matriz de accesibilidad de un Digrafo es:

Acc(D) = bin[In+ M+ M^2+ M^3+ ...+ M^n-1]

M es la matriz de conexión del digrafo, determinaremos M^2, M^3 hasta M^n-1donde n es el número de vértices del digrafo.

Luego de determinar las matrices antes mencionadas las sumaremos junto a la matriz identidad y ese resultado procederemos a binarizarlo (Los elementos mayores que 1 los haremos igual a 1, los elementos que sean igual a 0 seguirán siendo igual a 0).

Ejercicio de ejemplo:

Dada la matriz de conexión del siguiente digrafo, determinar su matriz de accesibilidad.

M=

M^2 = MxM

M^3 = M^2 * M

M^4 = M^3 * M

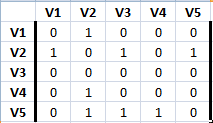
I5 =

Acc(D) = bin[In+ M+ M^2+ M^3+ ...+ M^n-1]

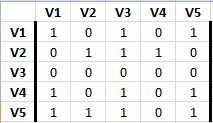
Acc(D) =

De esta manera podemos obtener la matriz de accesibilidad del digrafo. Este digrafo no es fuertemente conexo, debido a que su matriz de accesibilidad posee componentes nulas.

EnC++ Estos pasos para determinar sí el digrafo es F.C o no, los podemos realizar de la siguiente manera:

#include iostream

using namespace std;

int main(){
 int vertices;
 cout  "Ingrese la cantidad de vertices del digrafo:"  endl;
 cin  vertices;
 int matrizC[vertices][vertices];
 int matrizaux[vertices][vertices];
 int matrizM[vertices][vertices];
 int matrizAcc[vertices][vertices];
 //Cargamos la matriz de conexion
 cout  "Ingrese los elementos de la matriz de conexion: "  endl;
 for(int i = 0; i  vertices; i++){
  for(int j = 0; j  vertices; j++){
  cout  "Ingrese la entrada a"  i  j  endl;
  cin  matrizC[i][j];
  }
 }

   for(int i = 0; i  vertices; i++){
    for(int j = 0; j  vertices; j++){
     matrizaux[i][j] = matrizC[i][j];
     matrizAcc[i][j] = matrizC[i][j];
    }
   }
  //ciclo
  int cont = vertices-2;
  while(cont){
  // Producto para M...
   for(int i=0;ivertices;i++){
         for(int j=0;jvertices;j++){
             matrizM[i][j]=0;
           for(int k=0;kvertices;k++){
             matrizM[i][j]=matrizM[i][j]+(matrizC[i][k]*matrizaux[k][j]);
           }
     }
      }
  //Sumamos para la matriz de accesibilidad
   for(int i = 0; i  vertices; i++){
     for(int j = 0; j  vertices; j++){
     matrizAcc[i][j] += matrizM[i][j];
     matrizaux[i][j] =  matrizM[i][j];
     }
    }
   cont--;
  }//Fin del ciclo

  //Sumar matriz de indentidad y binarizar
  for(int i = 0; i  vertices; i++){
    for(int j = 0; j  vertices; j++){
    if(i == j)
     matrizAcc[i][j] = 1;
    if(matrizAcc[i][j]  1)
     matrizAcc[i][j] = 1;
    }
   }

  //Imprimimos la matriz de accesibilidad
  cout  "Matriz de accesibilidad:"  endl;
    for(int i = 0; i  vertices; i++){
      for(int j = 0; j  vertices; j++){
       cout  matrizAcc[i][j]  " ";
      }
      cout  endl;
    }


 return 0;
}

Inicialmente ingresamos el numero de vértices del digrafo, las matrices con las que vamos a trabajar son de orden nxn donde n es el numero de vértices del digrafo.

El ciclo while se repetirá mientras la variable cont sea distinta de 0 (n - 2 veces debido a que M^2 se calcula fuera del ciclo while), esta variable irá decreciendo de uno en uno en cada repetición del ciclo.

Mientras vamos realizando la multiplicación de las matrices vamos sumando los resultados en la matriz de accesibilidad.

Al final, luego de salir del ciclo sumamos la matriz identidad y binarizamos la matriz de accesibilidad.

Ejecución:

Ingrese la cantidad de vertices del digrafo:
5
Ingrese los elementos de la matriz de conexion:
Ingrese la entrada a00
0
Ingrese la entrada a01
1
Ingrese la entrada a02
0
Ingrese la entrada a03
0
Ingrese la entrada a04
0
Ingrese la entrada a10
1
Ingrese la entrada a11
0
Ingrese la entrada a12
1
Ingrese la entrada a13
0
Ingrese la entrada a14
1
Ingrese la entrada a20
0
Ingrese la entrada a21
0
Ingrese la entrada a22
0
Ingrese la entrada a23
0
Ingrese la entrada a24
0
Ingrese la entrada a30
0
Ingrese la entrada a31
1
Ingrese la entrada a32
0
Ingrese la entrada a33
0
Ingrese la entrada a34
0
Ingrese la entrada a40
0
Ingrese la entrada a41
1
Ingrese la entrada a42
1
Ingrese la entrada a43
1
Ingrese la entrada a44
0
Matriz de accesibilidad:
1 1 1 1 1
1 1 1 1 1
0 0 1 0 0
1 1 1 1 1
1 1 1 1 1

Descarga del proyecto en C++:
https://mega.co.nz/#!ZBETVRqK!eVh_8o...


También te podría interesar:
Algoritmo para calcular la matriz de la relación predecesor inmediato a partir de la matriz de la relación de orden en c++.
4 Ejercicios Básicos de Programación Orientada a Objetos en c++
eBook - Como programar en c++ Deitel
De sistema decimal a sistema binario en c++ y Java
3 libros sobre programacion orientada a objetos