En unaentradaanterior vimoscomo graficarecuaciones polares en MATLAB, ahora veremos algunas funciones que existen en MATLAB para realizar gráficas tanto en 2D como en 3D.
Plot(): Nos creará una gráfica 2D en nuestro plano cartesiano. Su sintaxis sería Plot(x,y) donde x e y son puntos en el plano. Estos puntos los crearemos con lafunción linspace, esta función crea un vector con un número de elementos determinados por nosotros, cuya distancia es igual para todos.
Ejemplo:
linspace(inicio del intervalo, fin del intervalo, cantidad de elementos del vector);
linspace(0,9,5);
0 y 9 sería el intervalo en que se encuentran los 5 elementos del vector que hemos creado, es decir el intervalo [0,9]. 5 obviamente es la cantidad de elementos.
Los elementos de nuestro vector serían: [0, 2.25, 4.5, 6.75, 9]
Graficando una parábola:
Para graficar una paráboladaremos valores a una variable x con la función linspace, es importante destacar que mientras mas puntos en el plano existan nuestra gráfica será mas precisa.
x = linspace(-3,3,100);
y = x.^2;
plot(x,y);
Este sería el resultado
En ocasiones resulta conveniente cambiar el color de nuestra gráfica, para ello agregaremos un parámetro mas a la función Plot(). Sería Plot(x,y,'color') donde color sería la inicial del nombre del color (en ingles) de nuestra gráfica, red, green, blue... Ejemplo Plot(x,y,'r') hará nuestra parábola de color rojo.
hold on Nos permitirá realizar varias gráficas en un mismo dibujo, podemos notar que si realizamos una nueva gráfica la anterior es eliminada del dibujo. Con la función hold on esto no sucederá. Para desactivar esta opción usamoshold off.
x = linspace(-3,3,100);
y = x.^2;
plot(x,y);
hold on
y = 5+ x.^2;
plot(x,y);
El resultado sería dos parábolas en nuestro dibujo.
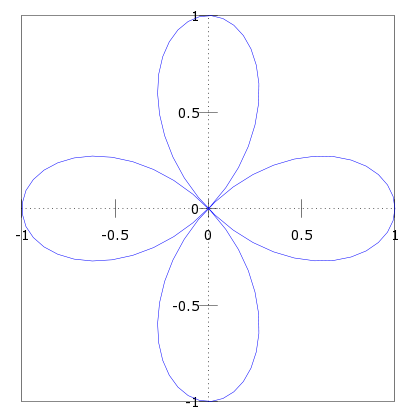
Polar(angulo,r)ya hablamos sobre esta función en la entradacomo graficarecuaciones polares en MATLABesta función graficará ecuaciones polares, un ejemplo de esto sería.
angulo = linspace(0,2*pi,100);r = cos(2*angulo);polar(angulo,r);fill(x,y,'color') nos permitirá realizar una gráfica cerrada pintada por dentro del color que indiquemos.x = linspace(-3,3,100);y = x.^2;fill(x,y,'g');El resultado seríaPlot3(x,y,z) similar a la función plot, solo que esta representará nuestras gráficas en 3D. Damos valores a x e y con la función linspace y evaluamos la función de dos variables, luego graficamos.
x = linspace(-3,3,100);y = linspace(-3,3,100);z = x.^2 + y.^2;plot3(x,y,z);Nuestra gráfica en 3D sería.Title('titulo') agrega un título a nuestra gráfica. Ejemplo, sí queremos agregar el título "Mi gráfica" a nuestra gráfica debemos escribir title('Mi Gráfica). En la siguiente imagen observaremos el resultado.
xlabel('texto') agregará una etiqueta o identificador al eje de las abscisas, para eliminarlo solo debemos escribir xlabel off. Para ylabel('texto') y zlabel('texto') es similar. Realicemos un ejemplo con esta función en MATLAB. Imaginemos que queremos representar gráficamente la cantidad de visitas que ha tenido nuestro blog en los últimos 7 días.
El eje de las abscisas (variable X) representará los días y el eje de las ordenadas (variable Y) representará la cantidad de visitas.
Vamos a crear dos vectores, para x será: x = [1 2 3 4 5 6 7] (los dias). Y para y será: y =[95 150 170 67 121 111 154] (cantidad de visitas en cada día).
Posterior a esto graficamos y utilizamos las etiquetas xlabel e ylabel. Nuestro programa y resultado sería el siguiente.
x = [1 2 3 4 5 6 7];y =[95 150 170 67 121 111 154];plot(x,y);xlabel('Dias');ylabel('Cant. Visitas');gtext('texto')nos permite agregar un texto en la gráfica haciendo click sobre esta, donde hayamos hecho click allí se colocará el texto indicado.
x = [1 2 3 4 5 6 7];y =[95 150 170 67 121 111 154];plot(x,y);xlabel('Dias');ylabel('Cant. Visitas');gtext('Ejemplo visitas');Algo que también podemos hacer es cambiar las líneas de nuestras gráficas, estas pueden ser punteadas, continuas y guiones. Para utilizarlas agregaremos un tercer parámetro a la función plot(x,y).
plot(x,y,'--') guiones, plot(x,y,'-') continua, plot(x,y,'-'), punteada plot(x,y,':').También te podría interesar:Aprendiendo MATLAB con Octave UPMGraficando ecuaciones polares en MATLAB con Octave UPM